This article builds on the articles on thermodynamics (article 2) and briefly introduces the issue of rheology, which is simply the study of material flow. In the following paragraphs, you will learn, for example, how water vortices are created or how the viscosity of substances is measured, and so on.
The following paragraphs provide a summary and introduction to the topic based on research from the following sources:
PRAGOLAB. Rheology Seminar. Prague: Pragolab 2015. Available at: http://www.pragolab.cz/files/download/Seminar_reologie_2015.pdf
PRUŠKA, J. Rheology, MH 8. Lecture. Prague: FS ČVUT 2008. Available at: http://departments.fsv.cvut.cz/k135/data/wp-upload/2008/05/reologie.pdf
HOLUBOVÁ, Renata. Basics of Rheology and Rheometry of Liquids. Olomouc: Palacký University Olomouc, 2014. ISBN 978-80-244-4178-8
Rheology is the study of the deformation and flow of materials; the movement of viscous (Newtonian) liquids and the transformation of masses. These masses are not perfectly elastic (Hooke’s material), nor fully ductile (St. Venant’s fluid), or flexible, but exhibit various combinations of these properties. Rheology is divided into macro-rheology and micro-rheology.
Macro-rheology – examines the deformable properties of matter from a general perspective.
Micro-rheology – studies the deformable properties of individual parts of matter.
Rheology deals with:
– The relationships between different types of deformation of materials and investigates the causes and effects of deformations,
– Relationships between shear stress and shear rate,
– The boundaries between liquids and solids.
Properties of Liquids
To describe the properties of ideal liquids, we define an ideal liquid as a liquid with no internal friction (non-viscous), with zero volume expansion and compressibility, zero gas solubility, and no evaporation.
Liquids are further divided according to (Holubová R.) into:
– Newtonian (e.g. water), where viscosity at a given temperature and pressure is a physical constant,
– Non-Newtonian (e.g. emulsions, mixtures of solid particles with liquids, paints), whose viscosity is not a physical constant.
Flow of real liquids is:
Laminated – particles move in layers that are mutually parallel, with no movement of particles perpendicular to the direction of motion;
Turbulent – particles have, in addition to the progressive speed, a turbulent (fluctuating) velocity, which is used to move along the cross-section.
Further in the area of liquid properties, the following relationships for stress are defined.
Normal stress (pressure) p – is given as the ratio of normal elemental force to the size of the given area:
p = dFn/ dS, (1)
where dS is the elemental area inside the liquid, and dFn is the normal component (acting perpendicular to the considered area) of the elemental force dF.
In a liquid, tensile stress cannot be induced, so pressure is measured as positive. When measuring pressure from zero value, it is referred to as the so-called absolute pressure. Sometimes it is advantageous to measure pressure from a certain reference pressure (usually atmospheric pressure). Pressure differences above or below this pressure are called overpressure and vacuum, respectively.
Shear stress τ – is given as the ratio of shear elemental force to the size of the given area:
τ = dFt/ dS, (2)
where dFt is the shear component (causing particle displacement in the liquid) of the elemental force dF acting on the elemental area dS.
For an elementary prism with height dy, where the lower wall moves with speed v and the upper wall moves with speed v + dv according to [11], the following applies:
τ = η dv/dy, (3)
Dynamic viscosity of liquids generally depends on temperature (decreases with increasing temperature) and pressure (the dependence is negligible). It manifests as resistance to particle movement in the liquid. Based on the dependence of dynamic viscosity on shear stress, liquids are divided into Newtonian (independent – equation (2)) and non-Newtonian (dependent – equation 3).
The dependence of viscosity on temperature can be expressed by the relationship:
η(T) = k * eb/(T+Θ), (4)
where constant k has the dimension of viscosity (Pa · s), b and Θ are constants characteristic for a given fluid, their unit is Kelvin.
The dependence of viscosity on pressure is expressed by the relationship:
η(p) = η0 * eαp, (5)
α is a coefficient dependent on temperature.
In addition to dynamic viscosity, we also introduce the quantity kinematic viscosity, which is defined by the relationship:
ν = η / ρ, (6)
where ρ is the density of the liquid.
Flow of liquid in a capillary – characteristic quantities for describing flow are: pressure difference Δp, capillary length l, and its radius r. In the stationary case, the pressure force Fp must equal the frictional force FR. For flow through a capillary, the velocity distribution is parabolic, meaning that the velocity v(r) forms a rotational paraboloid. The relationships for velocity profile and the amount of liquid flowing per unit time t are provided in the work.
Navier-Stokes Equation – represents the motion equation of a real flowing liquid. A real liquid is subject to gravitational, pressure, and frictional forces. The total force can be expressed as the sum of all acting forces. The goal is to find the distribution of velocities and pressures. Therefore, it is necessary to know the external acceleration, the density of the liquid, and the boundary conditions. The individual terms of the Navier-Stokes equation represent:
– external acceleration due to the effect of gravitational force,
– acceleration from surface (pressure) force,
– acceleration required to overcome viscous friction in liquids,
– acceleration due to viscosity in compressible liquids,
– convective acceleration from inertia force,
– local acceleration from inertia force.
For incompressible liquids, the fourth term of the equation (viscous acceleration) drops out due to the continuity equation. In a non-viscous liquid, the equation transitions to the Euler equation of hydrodynamics. Using the Navier-Stokes equation, classical hydrodynamics can be described. Unlike the Euler equation, it contains a term that expresses internal friction in the fluid.
The Navier-Stokes equation is a nonlinear differential equation. Its solution provides the distribution of velocities in the fluid depending on position and time. Mathematics does not have an analytical solution procedure for this equation; only special cases can be solved.
Laminated flow around a ball – viscous liquids exert force on any object moving within the liquid. It can be examined, for example, how to describe the fall of an object in a viscous liquid. Under the effect of gravitational force Fg, the object is accelerated, and its initial speed v0 = 0 continuously increases. The phenomenon lasts until the object reaches a constant velocity of fall v, i.e., the acceleration is zero. Then there is a balance between the downward gravitational force and the upward forces – buoyancy and friction: Fg = Fvz + FT.
Based on experiments with balls of different sizes and using various liquids, it was found that the frictional force depends on the coefficient η, final speed v, and the radius of the ball r, i.e. Stokes’ Law:
FT = -6πηrv. (7)
Vortices – a characteristic feature of turbulence is the formation of vortices. Imagine a cylinder being surrounded by fluid. From a certain flow velocity vG, stationary vortices with opposite rotation direction begin to form behind the cylinder in the so-called dead water zone. The vortex can be divided into two regions – the core and the circulation area. The explanation of vortex formation is carried out using a cylinder placed in the fluid, which moves from left to right and “collides” with the object – see the diagram.
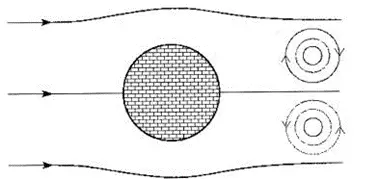
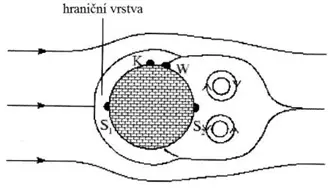
Newtonian Fluids
The viscosity of a Newtonian fluid depends only on temperature and follows a direct proportionality between shear stress and velocity gradient (Newton’s law of viscosity) (e.g., water, milk, sugar solution, mineral oils). In the case of an ideally viscous material, the classical Newtonian law holds for shear stress, see equation (3).Non-Newtonian Fluids
Time-dependent: – thixotropic (becoming thinner over time, viscosity decreases with time) – used in chemistry, food industry (yogurt), – rheopectic (becoming thicker over time, viscosity increases with time) – not common, examples include plaster, Time-independent: depends on temperature: – pseudoplastic (shear-thinning) – viscosity decreases with increasing shear stress (shampoo, concentrated juices, ketchup), – dilatant (shear-thickening) – viscosity increases with increasing shear stress (wet sand, concentrated starch suspensions), – plastic – have a yield point (curd, toothpaste).Rheological Measurement Methods
a) Absolute measurement – from Poiseuille’s law, we measure all other quantities, b) Relative measurement – comparison with a fluid whose dynamic viscosity is known – Ostwald viscometer, Höppler viscometer; Flow, falling, and rotational viscometers are commonly used to measure viscosity, with only the last type and special capillary viscometers providing sufficient characterization of the flow curve for non-Newtonian fluids. Proper measurement conditions always require laminar flow across the entire measurement range and a well-defined flow geometry (ability to determine D and τ) for non-Newtonian fluids.Measuring Devices Used in Rheology:
– Basic devices, – Capillary viscometers, – Falling ball viscometers, – Rotational viscometers, – Rotational rheometers, – Sensors – geometries, – Extensional rheometers, – Extrusion rheometers.| Principle | Device | Measured quantity |
| Volumetric flow | Ford funnel; capillary viscometer | Time; time (pressure, displacement) |
| Falling ball | Höppler viscometer | Time |
| Compression | Compression viscometer | Force, displacement |
| Rotation | Rotational viscometer, rheometer | Force, displacement |

