4.2 Data processing and analysis
For deriving dependencies in complex critical infrastructure, in the case of use, i.e., metro infrastructure, the sensitivity theory is applied in the presented work, which allows the strength of individual dependencies to be evaluated, i.e., their vulnerability, meaning the ability of dependencies to cause failure (KI, metro). The matrices are transformed into a graph for subsequent analysis.
4.2.1 Theory of sensitivity
For better interpretation and working with information systems, vulnerability can also be defined as sensitivity using sensitivity theory [87,88], which can be queried with the following relation [89]:
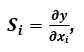
(22)
where Si is the absolute sensitivity of the output function y to the parameter of the input function xi. According to the source [90], in terms of electronic systems, y = f(x1,..,,xi,…,xN) is the network (or system) function, which depends on the circuit parameter xi. The change in the system’s output function is therefore dependent on its sensitivity and on the change in input parameters xi, and the relation is for practical reasons expressed in matrix form, i.e., using the sensitivity matrix S [90]:
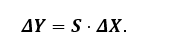
(23)
For electrical, electronic, and programmable electronic systems (hereinafter referred to as E/E/PE), it is advantageous to consider relative sensitivity and the relative change in parameters, as it allows for the calculation of output variable tolerances, the design of input parameter tolerances, optimization of circuit sensitivity, finding the most sensitive components, i.e., components with the greatest impact on changes in the output variable [90].
For working with assets, it is suitable to work with absolute sensitivity, because although the scales for evaluating criticality are normalized, each asset function has a different physical basis.
4.2.2 Matrix notation and codification of names
It is customary in practice to present the relationships of individual elements in tables. In our case, it concerns sensitivity, i.e., the relationship of input variables (hazards, i.e., assets) and output variables (system functions, i.e., assets):
For better clarity, a matrix notation is used, as shown in Table 8.
Table 8 Format of the asset criticality table for individual hazards.
| Hazard 1 | … | Hazard n | |
| Asset 1 | S11 | … | Sn1 |
| … | . | … | . |
| Asset m | S1m | … | Snm |
Table 8 is converted into matrix form, where yi represents assets and xi represents hazards. The matrix notation allows performing necessary operations and converting the matrix into a graph for scenario analysis.
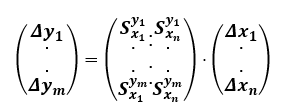
(24)
The input parameters xi can actually represent output parameters of other assets (functions). If we wish to display the relationships in greater depth, we can create a chain using both input and output parameters on both sides of the equation, i.e., for the purposes of this work, “chained sensitivity matrices,” which in engineering represent the degree of vulnerability dependent on the degree of interconnection of variables or parameters [6,33].
In practice, these tables and matrices can become large, and to ensure their readability, it is advisable to introduce an appropriate coding of names. The dissertation uses numerical designations for hazards listed in Appendix B. The designation of asset groups used is given in Table 9.
Table 9 Designation of asset groups used.
| Group | Designation |
| Construction | AK |
| Technology | AT |
| Personnel | AP |
| Locations | AM |
| Functions | AF |
| Connections and flows | AV |
| Organization and economy | AO |
The numerical designation of individual asset classes used below in the dissertation is due to their large scope provided in Appendix C.
4.2.3 Transformation of matrices into a graph
Using graph theory, as described, for example, in the work [91], vulnerabilities can be displayed using a weighted directed graph. To create the graph, the following steps are required:
- Use the sensitivity matrices mentioned in the previous sections 4.2.1 and 4.2.2,
- Transform the sensitivity matrices into adjacency matrices, which represent the degree of connection tightness of the observed variables. These matrices are the foundation for generating graphs that show the degrees of connection between the relevant variables.
For creating the adjacency matrices, the MS Excel tool is used, and the file with the matrices is then imported into a tool for working with graphs – Gephi 1Data processing and analysis, tool: G2 version 9.0.2 [92].
The graph transformation process can be broken down into the following steps:
- Creating adjacency matrices (measures of connection tightness) from sensitivity matrices (measures of vulnerability).
- Creating a directed graph – graphical interpretation.
- Rating the edges (vulnerability of the given link – connection) and nodes (vulnerability or criticality of the observed variables, assets).
- Analyzing the graph and graphical interpretation of the results.
4.2.3.1 Building adjacency matrices from sensitivity matrices
The adjacency matrix [91] expresses the relations between two objects (in this case, the input and output parameters of a function, or between nodes representing assets or hazards). Its columns and rows represent the same set of objects in the same sequence. To use the sensitivity matrices, it is necessary to start with the input parameters of the function and then with the output parameters of the function as follows: APdii02; ATv; Atzb; AVi06 (the used notations are explained in Appendix C).
According to matrix theory, we proceed by inserting the transposed sensitivity matrix into the empty adjacency matrix, and assuming that it is a basis for constructing a directed graph, where the relationships are one-way. In the other positions of the matrix, we fill in zeros “0”. Table 10 represents the resulting adjacency matrix, with the cells shaded in blue showing the transposed sensitivity matrix.
Table 10 Adjacency matrix for the relationship (44) (section 6.1.3).
| APdii02 | ATv | ATzb | AVi06 | |
| APdii02 | 0 | 0 | 0 | 1 |
| ATv | 0 | 0 | 0 | 1 |
| ATzb | 0 | 0 | 0 | 1 |
| AVi06 | 0 | 0 | 0 | 0 |
The algorithm can be applied to all previous simple relationships where certain input and output parameters are not shared. For concatenated matrices, it is necessary to consider the shared input and output parameters and carefully create the sequence of nodes. The notation for the concatenated matrix is shown in Table 11.
Table 11 Adjacency matrix for concatenated matrices (relationship (45) and section 6.1.3).
| AKs01 | AKk06 | ATv | AVi06 | ATe | AMtp03 | APdii02 | ATzb | AVm01 | |
| AKs01 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 |
| AKk06 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 |
| ATv | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0,5 |
| AVi06 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 |
| ATe | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 |
| AMtp03 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 |
| APdii02 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| ATzb | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| AVm01 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
4.2.3.2 Construction of an oriented graph - graphical interpretation
According to the definition in [91], the directed graph is represented by an ordered triplet:
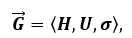
(25)
where H is the set of edges, U is the set of nodes, and σ is the incidence relation expressed by the formula:
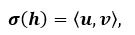
(26)
where u is the initial vertex and v is the terminal vertex. The graph G can be fully derived from the adjacency matrices [91]. The graph for Table 10 is shown in Figure 13, and for Table 11 in Figure 14.
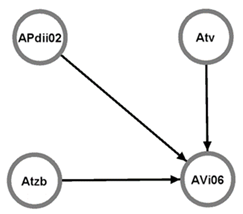
Figure 13. Graph for Table 3 (AVi06), [3].
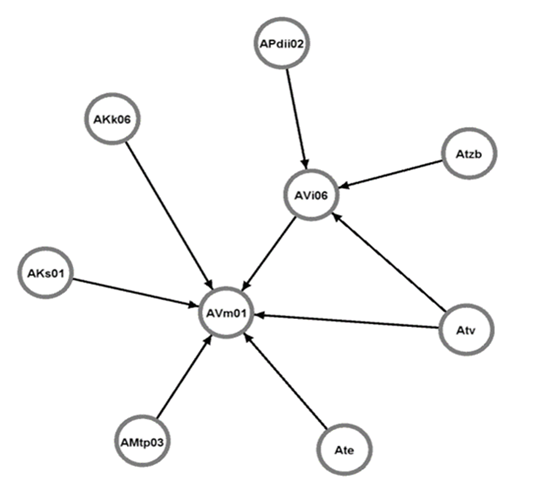
Figure 14. Graph for Table 4 (Avi06-m01), [3].
4.2.3.3 Evaluation of edges (vulnerability of a given link) and nodes (vulnerability or criticality)
Figures 13 and 14 represent the graphs according to the provided adjacency matrices, but they do not represent the weighting of edges and node parameters. Each edge and node can have the required information added in text form (weighting of the edge, or the vulnerability or criticality of the node). Using the software tool [92], these parameters can be graphically interpreted, i.e., changing the size or color of edges and nodes according to their properties.
The edge weight, for the purposes of this work, is the evaluation of the degree of connectivity, i.e., the sensitivity (or vulnerability) of the target asset to the input parameter (function of the asset or hazard).
Textual evaluation of nodes in the dissertation indicates the criticality, if needed for the given analysis (e.g., Figure 21 in paragraph 6.2.3).
Dimensions and colors of nodes and edges used in the dissertation are described in the following paragraph.
4.2.3.4 Graph analysis and graphical interpretation of results
The tool Gephi 0.9.2 was used to display the graph [92]. The default display (layout) of nodes on the workspace in the tool is not ideal, so it is necessary to adjust the layout accordingly. Manual placement of nodes can be used depending on the need and type of node, or known algorithms can also be applied. Additionally, it is advisable to adjust the color differentiation of nodes and edges and their size according to their degree, weights, and other parameters.
For the graph analysis, the following optional parameters were chosen, which the tool allows [92]:
- Layout:
- Force-directed Fruchterman-Reingold [93],
- Area: 10000; Gravity: 10; Speed 1, which influences the final layout of nodes and edges on the workspace (or canvas) in the software tool.
- Nodes:
- Size based on “In-degree”; min: 10; max: 50; exponentially, the stated setting will exponentially enlarge the nodes with more incoming edges on the workspace,
- Color based on “In-degree”; min: black; max: red; linearly, the setting will color nodes red that have more incoming edges on the workspace,
- “In-degree” represents the number of incoming edges to a given node, regardless of their weight,
- “Out-degree” represents the number of outgoing edges from a given node, regardless of their weight.
- Edges:
- By default, thickness is based on weight,
- Color based on “Weight”; min: black; max: red; linearly distributed between the minimum and maximum.

